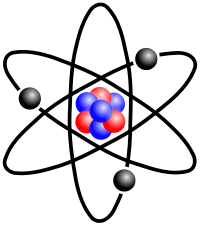
Are all the orbits of sub atomic particles ellipses? Do electrons circulate in elliptical orbits?
In geometry, an ellipse (from Greek ἔλλειψις elleipsis, a "falling short") is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis. An ellipse is also the locus of all points of the plane whose distances to two fixed points add to the same constant.
Ellipses are closed curves and are the bounded case of the conic sections, the curves that result from the intersection of a circular cone and a plane that does not pass through its apex; the other two (open and unbounded) cases are parabolas and hyperbolas.
Ellipses arise from the intersection of a right circular cylinder with a
plane that is not parallel to the cylinder's main axis of symmetry.
Ellipses also arise as images of a circle under parallel projection and the bounded cases of perspective projection, which are simply intersections of the projective cone with the plane of projection. It is also the simplest Lissajous figure, formed when the horizontal and vertical motions are sinusoids with the same frequency.
An ellipse is a smooth closed curve which is symmetric about its horizontal and vertical axes. The distance between antipodal points on the ellipse, or pairs of points whose midpoint is at the center of the ellipse, is maximum along the major axis or transverse diameter, and a minimum along the perpendicular minor axis or conjugate diameter.[1]
The semi-major axis (denoted by a in the figure) and the semi-minor axis (denoted by b in the figure) are one half of the major and minor axes, respectively. These are sometimes called (especially in technical fields) the major and minor semi-axes,[2][3] the major and minor semiaxes,[4][5] or major radius and minor radius.[6][7][8][9]
If the structure of an atom is an ellipse, it would provide a stable orbit with these mathematical properties, around the foci of the ellipse, for an electron. It would potentially explain much about the essential symmetry, and apparent lack of randomness about the atom, but we have yet to explain why Hydrogen can have these properties, with only one proton in the nucleus, not providing two points of focus.
The foci of the ellipse are two special points F1 and F2 on the ellipse's major axis and are equidistant from the center point. The sum of the distances from any point P on the ellipse to those two foci is constant and equal to the major axis ( PF1 + PF2 = 2a ). Each of these two points is called a focus of the ellipse.
An ellipse is the figure consisting of all those points
for which the sum of their distances to two fixed points (called the foci) is a constant.
This description of an ellipse is not the most useful if we
want to get detailed information about the ellipse such as the total
length around its perimeter or the total area it encloses.
For this level of detail we need to introduce the idea of coordinates
to describe all points in a flat 2-dimensional plane.
The coordinates we need are called Cartesian coordinates,
in honour of their inventor, René Descartes.
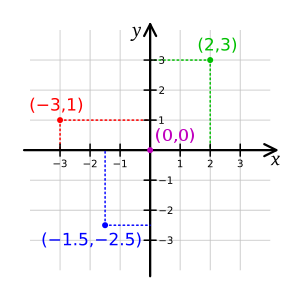
Imagine that our ellipse lies in a flat plane. On this plane we can draw two straight lines which intersect at right angles. Call one of these lines the x-axis, and call the other one the y-axis (it's not too important which is which). Call the point where the intersect the origin, and label it with the pair (0,0). For any other point in the plane, measure its perpendicular distance to the two axes, and call these x and y, as in the diagram. Label the point by the pair (x,y). These are called the Cartesian coordinates of the point. You can think of them as giving the address of the point (``to get to point (x,y), start at the origin, go a distance x along the x-axis, then go a distance y parallel to the y-axis. You can't miss it.'')
Our goal is to use Cartesian coordinates to get a convenient
description of all the points lying on an ellipse.
Given an ellipse, we can locate the

The ellipse and some of its mathematical properties.

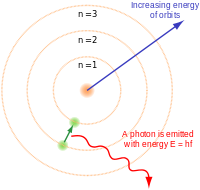
An electron (in an energy shell) orbiting a nucleus has one of these types of otbits; fig 1, fig 2, fig 3.
The electron could also pass through the centre of the nucleus.
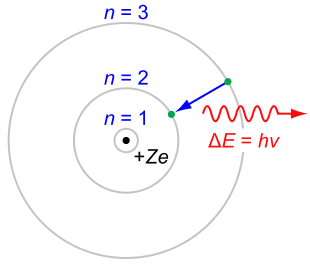
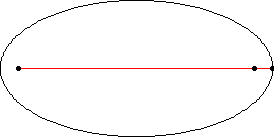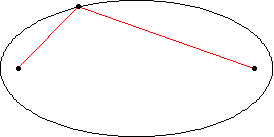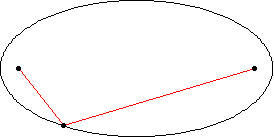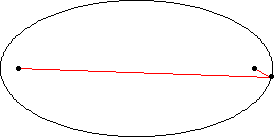
Figure 3

coordinate axes anywhere we
find convenient relative to the ellipse.
As you'll see, it makes sense to draw the x-axis through the two
foci of the ellipse, and to put the y-axis exactly midway between them,
as in the diagram. If the distance between the foci is D,
then their Cartesian coordinates will be (-D/2,0) for the one
and (+D/2, 0) for the other. Now consider any point on the ellipse,
and denote its coordinates by (x,y). By the definition of an ellipse,
we know that
Before we can go any further, we need to understand how
to compute the distance between any two points.
Suppose the points have coordinates (x,y) and (a,b). Then
(Remember that z1/2 means the square-root of z.)
If we apply this to our point on the ellipse,
then the defining condition tells us that
We can rearange this to read
Squaring both sides of this equation then leads to the formula
If we again square both sides of the equation and rearrange things a bit, we get
This looks a little neater if we use a to denote the quantity L/2, and use b to denote the quantity (L2-d2)1/2/2. The equation then becomes
and we arrive at the following definition of an ellipse:
An ellipse is the figure consisting of all points
in the plane whose Cartesian coordinates satisfy the equation
x2/a2
+ y2/b2 = 1
Related outside links
Famous curves applet (a java program which draws ellipses and other curves)
Figure 1 above, figure 2 below.

Diagram showing how an exoplanet orbiting a star produces changes in
position and velocity of the star as they orbit their common center of
mass (which is here the reference point)