mayfair

www.rainierbank.biz

$π,$ Radians and steradians

Here is a question for you.

You will see on this page some easy ways to calculate angles using radians, which have been summarised. Does this hold true for an ellipse?

In other words, if 360 degrees in a circle adds up to 2 times pi, does this hold true for an ellipse?

Imagine the area (steradian) -f, P, -a (P,-a)

or f, a, P (steradian a,P); if this ellipse with two foci was actually a circle with two foci. Why, because we can first.

$π$ (sometimes written pi) is a mathematical constant that is the ratio of any Euclidean^[1] circle's circumference to its diameter. $π$ is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve $π$ , which makes it one of the most important mathematical constants.^[2] For instance, the area of a circle is equal to $π$ times the square of the radius of the circle.

The circumference of a circle is slightly more than three times as long as its diameter. The exact ratio is called $π$ .

$π$ is an irrational number, which means that its value cannot be expressed exactly as a fraction having integers in both the numerator and denominator (unlike 22/7). Consequently, its decimal representation never ends and never repeats. $π$ is also a transcendental number, which implies, among other things, that no finite sequence of algebraic operations on integers (powers, roots, sums, etc.) can render its value; proving this fact was a significant mathematical achievement of the 19th century.

I've always had a bit of a problem with $π$ , and I don't mean eating it, I mean understanding it. I've always thought that despite the fact that it exists as an irrational number, somehow given the symmetry of the universe, it should be a whole number. One day I plan to resolve the problem. It could be as simple as coming up with a system of measurement which makes both the circumference and the diameter multiples of an exact unit. In the mean time, answer this question, how much bigger than a circle (or a sphere) would an ellipse have to be to make the circumference an exact (rational) number?

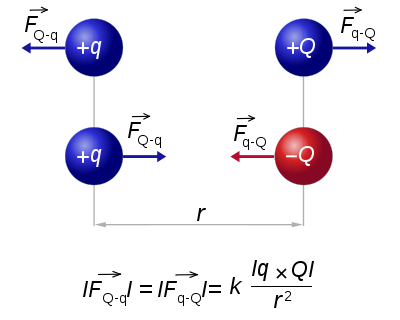
Diagram describing the basic mechanism of Coulomb's law; like charges repel each other and opposite charges attract each other.

In algebraic number theory, these commonly understood integers, embedded in the field of rational numbers, are referred to as rational integers to distinguish them from the more broadly defined algebraic integers (but with "rational" meaning "quotient of integers", this attempt at precision suffers from circularity).

Radians

Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit. The SI unit of solid angle measurement is the steradian.

A chart to convert between degrees and radians

In calculus and most other branches of mathematics beyond practical geometry, angles are universally measured in radians. This is because radians have a mathematical "naturalness" that leads to a more elegant formulation of a number of important results.

Most notably, results in analysis involving trigonometric functions are simple and elegant when the functions' arguments are expressed in radians. For example, the use of radians leads to the simple limit formula

$\lim_{h\rightarrow 0}\frac{\sin h}{h}=1,$

which is the basis of many other identities in mathematics, including

$\frac{d}{dx} \sin x = \cos x$

$\frac{d^2}{dx^2} \sin x = -\sin x.$

Because of these and other properties, the trigonometric functions appear in solutions to mathematical problems that are not obviously related to the functions' geometrical meanings (for example, the solutions to the differential equation 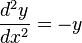$\frac{d^2 y}{dx^2} = -y$ , the evaluation of the integral 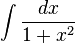$\int \frac{dx}{1+x^2}$ , and so on). In all such cases it is found that the arguments to the functions are most naturally written in the form that corresponds, in geometrical contexts, to the radian measurement of angles.

Steridans

The steradian (symbol: sr) is the SI unit of solid angle. It is used to describe two-dimensional angular spans in three-dimensional space, analogous to the way in which the radian describes angles in a plane. The name is derived from the Greek stereos for "solid" and the Latin radius for "ray, beam".

A steradian can be defined as the solid angle subtended at the center of a unit sphere by a unit area on its surface. For a general sphere of radius r, any portion of its surface with area A = r² subtends one steradian.^[1]

In two dimensions, the angle in radians is related to the arc length it cuts out:

$\theta = \frac{l}{r} \,$

where

l is arc length, and

r is the radius of the circle.

Now in three dimensions, the solid angle in steradians is related to the area it cuts out:

$\Omega = \frac{S}{r^2} \,$

where

S is the surface area, and

r is the radius of the sphere.

Arc segment

Determining the length of an irregular arc segment is also called rectification of a curve. Historically, many methods were used for specific curves. The advent of infinitesimal calculus led to a general formula that provides closed-form solutions in some cases.

Approximation by multiple linear segments

A curve in the plane can be approximated by connecting a finite number of points on the curve using line segments to create a polygonal path. Since it is straightforward to calculate the length of each linear segment (using the Pythagorean theorem in Euclidean space, for example), the total length of the approximation can be found by summing the lengths of each linear segment.

An angle of 1 radian results in an arc with a length equal to the radius of the circle.

Some common angles, measured in radians. All the polygons are regular polygons.

Steradians

The steradian, like the radian, is dimensionless because 1 sr = m²·m⁻² = 1. It is useful, however, to distinguish between dimensionless quantities of different nature, so in practice the symbol "sr" is used where appropriate, rather than the derived unit "1" or no unit at all. For example, radiant intensity can be measured in watts per steradian (W·sr⁻¹). The steradian was formerly an SI supplementary unit, but this category was abolished from the SI in 1995 and the steradian is now considered an SI derived unit.

A graphical representation of 1 steradian. The sphere has radius r, and in this case the area of the patch on the surface is A = r². The solid angle is θ = A/r² so in this case θ = 1. The entire sphere has a solid angle of 4π sr ≈ 12.56637 sr.

Section of cone (1) and spherical cap (2) inside a sphere

Since A = r², it corresponds to the area of a spherical cap (A = 2πrh) (wherein h stands for the "height" of the cap), and the relationship h/r = 1/(2π) holds. Therefore one steradian corresponds to the plane (i.e. radian) angle of the cross-section of a simple cone subtending the plane angle 2θ, with θ given by:

This angle corresponds to the plane aperture angle of 2θ ≈ 1.144 rad or 65.54°.

Because the surface area of a sphere is 4πr², the definition implies that a sphere measures 4π ≈ 12.56637 steradians. By the same argument, the maximum solid angle that can be subtended at any point is 4π sr. A steradian can also be called a squared radian.

A steradian is also equal to the spherical area of a polygon having an angle excess of 1 radian, to 1/(4π) of a complete sphere, or to (180/π)² ≈ 3282.80635 square degrees.

The solid angle (in steradians) subtended by the cone above (whose cross-section subtends the radian angle 2θ) is given by:

$\Omega = 2\pi(1 - \cos\theta).\quad$

Steradians only go up to 4π ≈ 12.56637, so the large multiples are not usable for the base unit, but could show up in such things as rate of coverage of solid angle, for example.

10¹	decasteradian	dasr	Slightly more than the surface area of all water on Earth, relative to Earth

10⁻¹⁵	femtosteradian	fsr	Area of a sheet of A5 paper, relative to Earth

10⁻²⁴	yoctosteradian	ysr	Surface area of a red blood cell, relative to Earth

protons 58