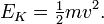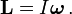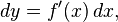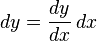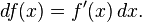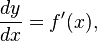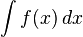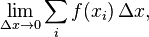mayfair

www.rainierbank.biz

Angular Momentum of light

Compare these two equations:
Energy is equal to mass times velocity;
where mass is equal to any mass (in kilograms) and
velocity is equal to c squared, (the speed of light, or the distance covered by (displacement of) a photon divided by the unit time, multiplied by itself (the distance travelled by a photon divided by unit time).
Or; (alternately)
Mass divided by volume is equal to energy;
Where volume is the wavelength of light and
mass is equal to mass of one photon.
"The kinetic energy (energy of motion),

E K

, of a moving object is linear with both its mass and the square of its velocity:"

$E_{K} = \begin{matrix} \frac{1}{2} \end{matrix} mv^2.$

The energy of an object increases proportionally according to its increasing velocity. A mass of mass M travelling at 2 x X, will have twice the kinetic energy of a mass travelling at 1 X. The total momentum of an object is equal to its mass times its velocity. To extract the total energy from that mass, you must break it down into its smallest constituent parts: light or photons, which will be travelling at speed C; the velocity of light.

Think about E= M squared,
(from Newton's E= 1/2 mv squared- something he proved, and derrived from actual observations of masses rotating around bodies)
or E = Mass times volume, where mass = 1 photon, and volume = wavelength of light,
or cubed (to give it three dimensions, length, breadth and height (and possibly one more beside).
What Newton failed to see, because he had no insight into the inside of the atom, was what Einstein revealed with his Special and General Relativity. Both Newton (although he may have fudged a little on gravity- in order to get us to Mars) and Einstein were right, which scientists have proven, but we have moved on since then.

All light travels at the speed of light 'c' where: -
c = λ x f
With 'f' as the frequency of the light.

Einstein showed that light may also be modelled as small quanta or photons of energy 'E' given by: -
E = hf
Where 'h' is Planck's constant.

Newton

In Newtonian mechanics, the kinetic energy (energy of motion), $E K$ , of a moving object is linear with both its mass and the square of its velocity:

$E_{K} = \begin{matrix} \frac{1}{2} \end{matrix} mv^2.$

The kinetic energy is a scalar quantity.

The Newton-Leibniz approach to infinitesimal calculus was introduced in the 17th century. While Newton did not have a standard notation for integration, Leibniz began using the 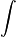$\int$ character. He based the character on the Latin word summa ("sum"), which he wrote ſumma with the elongated s commonly used in Germany at the time. This use first appeared publicly in his paper De Geometria, published in Acta Eruditorum of June 1686,^[2] but he had been using it in private manuscripts at least since 1675.^[3]

Velocity

In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant direction typically constrains the object to motion in a straight path. A car moving at a constant 20 kilometers per hour in a circular path does not have a constant velocity. The rate of change in velocity is acceleration. Velocity is a vector physical quantity; both magnitude and direction are required to define it. The scalar absolute value (magnitude) of velocity is speed, a quantity that is measured in metres per second (m/s or ms⁻¹) when using the SI (metric) system.

For example, "5 metres per second" is a scalar and not a vector, whereas "5 metres per second east" is a vector. The average velocity v of an object moving through a displacement 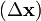$( \Delta \mathbf{x})$ during a time interval $(Δ t)$ is described by the formula:

$\mathbf{\bar{v}} = \frac{\Delta \mathbf{x}}{\Delta t}.$

The rate of change of velocity is acceleration – how an object's speed or direction of travel changes over time, and how it is changing at a particular point in time.

Angular Momentum

In physics, angular momentum, moment of momentum, or rotational momentum^[1]^[2] is a vector quantity that can be used to describe the overall state of a physical system. The angular momentum L of a particle with respect to some point of origin is

$\mathbf{L} = \mathbf{r} \times \mathbf{p} = \mathbf{r} \times m\mathbf{v}\, ,$

where r is the particle's position from the origin, p = mv is its linear momentum, and × denotes the cross product.

The angular momentum of a system of particles (e.g. a rigid body) is the sum of angular momenta of the individual particles. For a rigid body rotating around an axis of symmetry (e.g. the fins of a ceiling fan), the angular momentum can be expressed as the product of the body's moment of inertia I (a measure of an object's resistance to changes in its rotation rate) and its angular velocity ω:

$\mathbf{L} = I \boldsymbol{\omega} \, .$

In this way, angular momentum is sometimes described as the rotational analog of linear momentum.

Angular momentum is conserved in a system where there is no net external torque, and its conservation helps explain many diverse phenomena. For example, the increase in rotational speed of a spinning figure skater as the skater's arms are contracted is a consequence of conservation of angular momentum. The very high rotational rates of neutron stars can also be explained in terms of angular momentum conservation. Moreover, angular momentum conservation has numerous applications in physics and engineering (e.g. the gyrocompass).

What then is the problem? Can we identify it? The problem, if it exists at all it is

Does light (a photon) have spin? If it does, how much, and how does this affect the amount of energy a photon has?

Time

Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects.^[1] The temporal position of events with respect to the transitory present is continually changing; events happen, then are located further and further in the past. Time has been a major subject of religion, philosophy, and science, but defining it in a non-controversial manner applicable to all fields of study has consistently eluded the greatest scholars. A simple definition states that "time is what clocks measure".

Time is one of the seven fundamental physical quantities in the International System of Units. Time is used to define other quantities — such as velocity — so defining time in terms of such quantities would result in circularity of definition.^[2] An operational definition of time, wherein one says that observing a certain number of repetitions of one or another standard cyclical event (such as the passage of a free-swinging pendulum) constitutes one standard unit such as the second, is highly useful in the conduct of both advanced experiments and everyday affairs of life. The operational definition leaves aside the question whether there is something called time, apart from the counting activity just mentioned, that flows and that can be measured. Investigations of a single continuum called spacetime bring questions about space into questions about time, questions that have their roots in the works of early students of natural philosophy.

Calculus

The modern development of calculus is usually credited to Isaac Newton (1643–1727) and Gottfried Leibniz (1646–1716), who provided independent^[7] and unified approaches to differentiation and derivatives. The key insight, however, that earned them this credit, was the fundamental theorem of calculus relating differentiation and integration: this rendered obsolete most previous methods for computing areas and volumes,^[8] which had not been significantly extended since the time of Ibn al-Haytham (Alhazen).^[9] For their ideas on derivatives, both Newton and Leibniz built on significant earlier work by mathematicians such as Isaac Barrow (1630–1677), René Descartes (1596–1650), Christiaan Huygens (1629–1695), Blaise Pascal (1623–1662) and John Wallis (1616–1703). Isaac Barrow is generally given credit for the early development of the derivative.^[10] Nevertheless, Newton and Leibniz remain key figures in the history of differentiation, not least because Newton was the first to apply differentiation to theoretical physics, while Leibniz systematically developed much of the notation still used today.

Since the 17th century many mathematicians have contributed to the theory of differentiation. In the 19th century, calculus was put on a much more rigorous footing by mathematicians such as Augustin Louis Cauchy (1789–1857), Bernhard Riemann (1826–1866), and Karl Weierstrass (1815–1897). It was also during this period that the differentiation was generalized to Euclidean space and the complex plane.

Calclus

In calculus, the differential represents the principal part of the change in a function y = ƒ(x) with respect to changes in the independent variable. The differential dy is defined by

$dy = f'(x)\,dx,$

where $f'(x)$ is the derivative of ƒ with respect to x, and dx is an additional real variable (so that dy is a function of x and dx). The notation is such that the equation

$dy = \frac{dy}{dx}\, dx$

holds, where the derivative is represented in the Leibniz notation dy/dx, and this is consistent with regarding the derivative as the quotient of the differentials. One also writes

$df(x) = f'(x)\,dx.$

The precise meaning of the variables dy and dx depends on the context of the application and the required level of mathematical rigor. The domain of these variables may take on a particular geometrical significance if the differential is regarded as a particular differential form, or analytical significance if the differential is regarded as a linear approximation to the increment of a function. In physical applications, the variables dx and dy are often constrained to be very small ("infinitesimal").

Leibniz's notation

In calculus, Leibniz's notation, named in honor of the 17th-century German philosopher and mathematician Gottfried Wilhelm Leibniz, uses the symbols dx and dy to represent "infinitely small" (or infinitesimal) increments of x and y, just as Δx and Δy represent finite increments of x and y.^[1] For y as a function of x, or

$y=f(x) \,,$

the derivative of y with respect to x, which later came to be viewed as

$\lim_{\Delta x\rightarrow 0}\frac{\Delta y}{\Delta x} = \lim_{\Delta x\rightarrow 0}\frac{f(x + \Delta x)-f(x)}{(x + \Delta x)-x},$

was, according to Leibniz, the quotient of an infinitesimal increment of y by an infinitesimal increment of x, or

$\frac{dy}{dx}=f'(x),$

where the right hand side is Lagrange's notation for the derivative of f at x. From the point of view of modern infinitesimal theory, $Δ x$ is an infinitesimal x-increment, $Δ y$ is the corresponding y-increment, and the derivative is the standard part of the infinitesimal ratio:

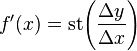$f'(x)={\rm st}\Bigg( \frac{\Delta y}{\Delta x} \Bigg)$ .

Then one sets $d x = Δ x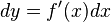$ , $dy = f'(x) dx\,$ , so that by definition, 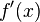$f'(x)\,$ is the ratio of dy by dx.

Similarly, although mathematicians sometimes now view an integral

$\int f(x)\,dx$

as a limit

$\lim_{\Delta x\rightarrow 0}\sum_{i} f(x_i)\,\Delta x,$

where Δx is an interval containing x_i, Leibniz viewed it as the sum (the integral sign denoting summation) of infinitely many infinitesimal quantities f(x) dx. From the modern viewpoint, it is more correct to view the integral as the standard part of an infinite sum of such quantities.

In mathematical physics, Equations of motion are equations that describe the behaviour of a physical system in terms of its motion as a function of time.^[1] More specifically, they are usually differential equations in terms of some function of dynamic variables: normally spatial coordinates and time are used, but others are also possible, such as momentum components and time. The most general choice are generalized coordinates which can be any convenient variables characteristic of the physical system.^[2]

There are two main descriptions of motion: dynamics and kinematics. Dynamics is general, since momenta, forces and energy of the particles are taken into account. In this instance sometimes the term refers to the differential equations that the system satisfies (e.g., Newton's second law or Euler–Lagrange equations), and sometimes to the solutions to those equations.

protons 53