It is said that like charges repel, unlike charges attract, but why?
The diagram at left shows like charges attracting (blue) and unlike (red and blue- positive and negatice) charges repelling. The mathematics proves it, or describes it, but that is too complicated for us. Why do like charges repel? If gravity (of two equal masses) attracts, why does it not repel? Why does it only happen with charged particles, or does it have something to do with electric field lines? What is going on?
Follow the algebra in these illustrations if you like, but don't worry if it is too hard. You can trust that it is right, and come back to it later.
Coulomb's Law
The scalar form of Coulomb's law is an expression for the magnitude and sign of the electrostatic force between two idealized point charges, small in size compared to their separation. This force (F) acting simultaneously on point charges (q1) and (q2), is given by
where r is the separation distance and ke is a proportionality constant. A positive force implies it is repulsive, while a negative force implies it is attractive.[7] The proportionality constant ke, called the Coulomb constant (sometimes called the Coulomb force constant), is related to defined properties of space and can be calculated based on the speed of light to be exactly:[8]

Coulomb's law states that: "The magnitude of the Electrostatics force of interaction between two point charges is directly proportional to the scalar multiplication of the magnitudes of charges and inversely proportional to the square of the distances between them."
In SI units, the meter is defined such that the speed of light in vacuum (or electromagnetic waves, in general), denoted c,[9] is exactly 299,792,458 m·s−1[10], and the magnetic constant (μ0) is set at 4π × 10−7 H·m−1.[11] In agreement with electromagnetic theory, requiring that
the value for the electric constant (ε0) is derived to be ε0 = 1/(μ0c2) ≈ 8.85418782×10−12 F·m−1.[12] In electrostatic units and Gaussian units, the unit charge (esu or statcoulomb) is defined in such a way that the Coulomb constant is 1 and dimensionless.
In the more useful vector-form statement, the force in the equation is a vector force acting on either point charge, so directed as to push it away from the other point charge; the right-hand side of the equation, in this case, must have an additional product term of a unit vector pointing in one of two opposite directions, e.g., from q1 to q2 if the force is acting on q2; the charges may have either sign and the sign of their product determines the ultimate direction of that force. Thus, the vector force pushing the charges away from each other (pulling towards each other if negative) is directly proportional to the product of the charges and inversely proportional to the square of the distance between them. The square of the distance part arises from the fact that the force field due to an isolated point charge is uniform in all directions and gets "diluted" with distance as much as the area of a sphere centered on the point charge expands with its radius.
The law of superposition allows this law to be extended to include any number of point charges, to derive the force on any one point charge by a vector addition of these individual forces acting alone on that point charge. The resulting vector happens to be parallel to the electric field vector at that point, with that point charge (or "test charge") removed.
Coulomb's law can also be interpreted in terms of atomic units with the force expressed in Hartrees per Bohr radius, the charge in terms of the elementary charge, and the distances in terms of the Bohr radius.
Electric field
It follows from the Coulomb's Law that the magnitude of the electric field (E) created by a single point charge (q) at a certain distance (r) is given by:
For a positive charge, the direction of the electric field points along lines directed radially away from the location of the point charge, while the direction is the opposite for a negative charge. The SI units of electric field are volts per meter or newtons per coulomb.
In mathematics, scalar multiplication is one of the basic operations defining a vector space in linear algebra[1][2][3] (or more generally, a module in abstract algebra[4][5]). In an intuitive geometrical context, scalar multiplication of a real Euclidean vector by a positive real number multiplies the magnitude of the vector without changing its direction. The term "scalar" itself derives from this usage: a scalar is that which scales vectors. Scalar multiplication is different from the scalar product, which is an inner product between two vectors.
There is a simpler explanation for the non-scientific among you, of why charges act the way they do, and we shall go into more detail on the next page.
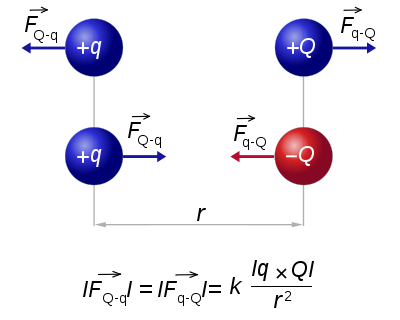
Diagram describing the basic mechanism of Coulomb's law; like charges repel each other and opposite charges attract each other.
(Diag, Three-dimensional Euclidean space; left)
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions. The term “Euclidean” distinguishes these spaces from the curved spaces of non-Euclidean geometry and Einstein's general theory of relativity, and is named for the Greek mathematician Euclid of Alexandria.
From the modern viewpoint, there is essentially only one Euclidean space of each dimension. In dimension one this is the real line; in dimension two it is the Cartesian plane; and in higher dimensions it is the real coordinate space with three or more real number coordinates. Thus a point in Euclidean space is a tuple of real numbers, and distances are defined using the Euclidean distance formula. Mathematicians often denote the n-dimensional Euclidean space by  , or sometimes
, or sometimes  if they wish to emphasize its Euclidean nature. Euclidean spaces have finite dimension.
if they wish to emphasize its Euclidean nature. Euclidean spaces have finite dimension.
Since Euclidean space is a metric space it is also a topological space with the natural topology induced by the metric. The metric topology on En is called the Euclidean topology. A set is open in the Euclidean topology if and only if it contains an open ball around each of its points. The Euclidean topology turns out to be equivalent to the product topology on Rn considered as a product of n copies of the real line R (with its standard topology).
An important result on the topology of Rn, that is far from superficial, is Brouwer's invariance of domain. Any subset of Rn (with its subspace topology) that is homeomorphic to another open subset of Rn is itself open. An immediate consequence of this is that Rm is not homeomorphic to Rn if m ≠ n — an intuitively "obvious" result which is nonetheless difficult to prove.
Euclidean Vector
In elementary mathematics, physics, and engineering, a Euclidean vector (sometimes called a geometric[1] or spatial vector,[2] or – as here – simply a vector) is a geometric object that has both a magnitude (or length) and direction. A Euclidean vector is frequently represented by a line segment with a definite direction, or graphically as an arrow, connecting an initial point A with a terminal point B,[3] and denoted by 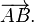
A vector is what is needed to "carry" the point A to the point B; the Latin word vector means "carrier".[4] The magnitude of the vector is the distance between the two points and the direction refers to the direction of displacement from A to B. Many algebraic operations on real numbers such as addition, subtraction, multiplication, and negation have close analogues for vectors, operations which obey the familiar algebraic laws of commutativity, associativity, and distributivity. These operations and associated laws qualify Euclidean vectors as an example of the more generalized concept of vectors defined simply as elements of a vector space.
Vectors play an important role in physics: velocity and acceleration of a moving object and forces acting on it are all described by vectors. Many other physical quantities can be usefully thought of as vectors. Although most of them do not represent distances (such as position or displacement), their magnitude and direction can be still represented by the length and direction of an arrow. The mathematical representation of a physical vector depends on the coordinate system used to describe it. Other vector-like objects that describe physical quantities and transform in a similar way under changes of the coordinate system include pseudovectors and tensors.
Scalars
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector.[1][2][3]
More generally, a vector space may be defined by using any field instead of real numbers, such as complex numbers. Then the scalars of that vector space will be the elements of the associated field.
Also, a scalar product operation (not to be confused with scalar multiplication) may be defined on a vector space, allowing two vectors to be multiplied to produce a scalar. A vector space equipped with a scalar product is called an inner product space.
The real component of a quaternion is also called its scalar part.
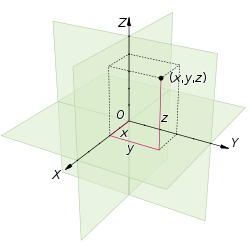
Every point in three-dimensional Euclidean space is determined by three coordinates.

Graphical representation of quaternion units product as 90°-rotation in 4D-space, ij = k, ji = −k, ij = −ji
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space. A feature of quaternions is that the product of two quaternions is noncommutative. Hamilton defined a quaternion as the quotient of two directed lines in a three-dimensional space[1] or equivalently as the quotient of two vectors.[2] Quaternions can also be represented as the sum of a scalar and a vector.
Quaternions find uses in both theoretical and applied mathematics, in particular for calculations involving three-dimensional rotations such as in three-dimensional computer graphics and computer vision. They can be used alongside other methods, such as Euler angles and matrices, or as an alternative to them depending on the application.
Quaternion plaque on Brougham (Broom) Bridge, Dublin, which says:
on the 16th of October 1843
Sir William Rowan Hamilton
in a flash of genius discovered
the fundamental formula for
quaternion multiplication
i2 = j2 = k2 = ijk = −1
& cut it on a stone of this bridge
From the mid-1880s, quaternions began to be displaced by vector analysis, which had been developed by Josiah Willard Gibbs, Oliver Heaviside, and Hermann von Helmholtz. Vector analysis described the same phenomena as quaternions, so it borrowed some ideas and terminology liberally from the literature of quaternions. However, vector analysis was conceptually simpler and notationally cleaner, and eventually quaternions were relegated to a minor role in mathematics and physics. A side-effect of this transition is that Hamilton's work is difficult to comprehend for many modern readers. Hamilton's original definitions are unfamiliar and his writing style was prolix and opaque.



