mayfair

www.rainierbank.biz

Atoms

The shortest distance between two points is a straight line.

Here is a series or numbers. Call it an intelligence test if you like. .5, 2, 5... What are thenext two or three numbers in the series?

.5 x 4 = 2

2 x 2.5 = 5

Say the next number in the series is 10, because it is a prediction, and thses numbers represent averave temperatures worldwide. Can we say that in year one, average temperature increase was .5 of a degree, in year twoit was 2 degrees and in year three, 5 degrees, representing a 7.5 degree increase in three years. Would this mean a possible increase of 17.5 degrees in four years?

Here is another problem. (when I remember what it was).

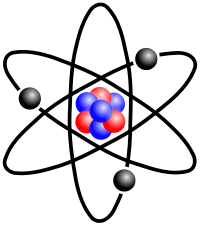
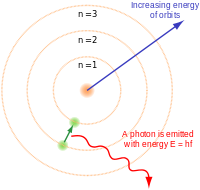
In the (sphere) below, can you see three planes, or six planes? There are 12 points on the surface of the sphere, if you can imagine it as a balloon filled with Helium. If the six planes are reduced to six particles (electrons) orbiting a central point, can you then imagine that the circular, (or eliptical) orbit has just six points on the outside surface of the sphere. I'm not going to labour this point, just in case you understand it. It can represent any particle, from a proton to a photon, not necessarily an electron.

This spherical shape can be further reduced to a geodesic triangle on a sphere, or alternately, a sphere composed of eight triangles (triangular pyramids) with a point in the centtre, and a radian on teh surface, if you imagine that a particle orbiting around the central point does not bneed to occupy all the area on teh surface of the sphere, but simply maintain 'pressure' (like charges repel, unlike charges attract) to define the boundary, or surface. The inverse square law applies, (as the distance from the centre of mass increases, the effective charge decreases), but the orbiting particle remains bound to the central point by gravity, (angular mementum) until it either gains or loses energy (velocity, or acceleration).

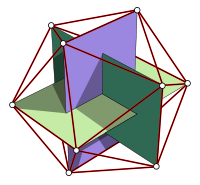
The following Cartesian coordinates define the vertices of an icosahedron with edge-length 2, centered at the origin:^[1]

(0, ±1, ±φ)

(±1, ±φ, 0)

(±φ, 0, ±1)

where φ = (1 + √5) / 2 is the golden ratio (also written τ). Note that these vertices form five sets of three concentric, mutually orthogonal golden rectangles, whose edges form Borromean rings.

If the original icosahedron has edge length 1, its dual dodecahedron has edge length $\tfrac{\sqrt{5}-1}{2}$ , one divided by the golden ratio.

Geodesic

In mathematics, particularly differential geometry, a geodesic ( /ˌdʒiːɵˈdiːzɨk/ jee-o-dee-zik or /ˌdʒiːɵˈdɛsɨk/ jee-o-des-ik) is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be (locally) the shortest path between points in the space. In the presence of an affine connection, geodesics are defined to be curves whose tangent vectors remain parallel if they are transported along it.

The term "geodesic" comes from geodesy, the science of measuring the size and shape of Earth; in the original sense, a geodesic was the shortest route between two points on the Earth's surface, namely, a segment of a great circle. The term has been generalized to include measurements in much more general mathematical spaces; for example, in graph theory, one might consider a geodesic between two vertices/nodes of a graph.

Geodesics are of particular importance in general relativity, as they describe the motion of inertial test particles.

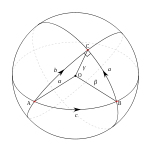
A geodesic triangle on the sphere. The geodesics are great circle arcs.

The shortest path between two points in a curved space can be found by writing the equation for the length of a curve (a function f from an open interval of R to the manifold), and then minimizing this length using the calculus of variations. This has some minor technical problems, because there is an infinite dimensional space of different ways to parameterize the shortest path. It is simpler to demand not only that the curve locally minimize length but also that it is parameterized "with constant velocity", meaning that the distance from f(s) to f(t) along the geodesic is proportional to |s−t|. Equivalently, a different quantity may be defined, termed the energy of the curve; minimizing the energy leads to the same equations for a geodesic (here "constant velocity" is a consequence of minimisation). Intuitively, one can understand this second formulation by noting that an elastic band stretched between two points will contract its length, and in so doing will minimize its energy. The resulting shape of the band is a geodesic.

In mathematics, the antipodal point of a point on the surface of a sphere is the point which is diametrically opposite to it — so situated that a line drawn from the one to the other passes through the centre of the sphere and forms a true diameter.

Test particle

In physical theories, a test particle is an idealized model of an object whose physical properties (usually mass, charge, or size) are assumed to be negligible except for the property being studied, which is considered to be insufficient to alter the behavior of the rest of the system. The concept of a test particle often simplifies problems, and can provide a good approximation for physical phenomena. In addition to its uses in the simplification of the dynamics of a system in particular limits, it is also used as a diagnostic in computer simulations of physical processes.

The easiest case for the application of a test particle arises in Newtonian gravity. The general expression for the gravitational force between two masses $m 1$ and $m 2$ is:

$F(r) = -G \frac{m_1 m_2}{(r_1-r_2)^2}$

where $r 1$ and $r 2$ represent the position of each particle in space. In the general solution for this equation, both masses rotate around their center of mass, in this specific case:

$R = \frac{m_1r_1+m_2r_2}{m_1+m_2}$ ^[1]

In the case where one of the masses is much larger than the other ( $m 1 > > m 2$ ), one can assume that the smaller mass moves as a test particle in a gravitational field generated by the larger mass, which does not accelerate. By defining the gravitational field as

$g(r) = \frac{Gm_1}{r^2}$

with $r$ as the distance between the two objects, the equation for the motion of the smaller mass reduces to

$a(r) = \frac{F(r)}{m_2} = -g(r)$

and thus only contains one variable, for which the solution can be calculated more easily. This approach gives very good approximations for many practical problems, e.g. the orbits of satellites, whose mass is relatively small compared to that of the earth.

In simulations with electromagnetic fields the most important characteristics of a test particle is its electric charge and its mass. In this situation it is often referred to as a test charge.

An electric field is defined by $\textbf{E} = k\frac{q}{r^2} \hat{r}$ . Multiplying the field by a test charge $q test$ gives an electric force exerted by the field on a test charge. Note that both the force and the electric field are vector quantities, so a positive test charge will experience a force in the direction of the electric field.

In a magnetic field, the behavior of a test charge is determined by effects of special relativity described by the Lorentz force. In this case, a positive test charge will be deflected clockwise if moving perpendicular to a magnetic field pointing toward you, and counterclockwise if moving perpendicular to a magnetic field directed away from you.

protons 71