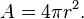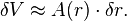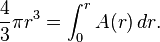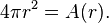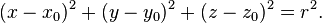mayfair

www.rainierbank.biz

Index

Site

The reason I believe that the relationship between the first element (Hydrogen) in the periodic table, and the second, (Helium) is 1 to 4 (Hydrogen has one proton, and Helium has 2 protons and 2 neutrons, bringing its mass to a ratio of 1 to 4, is because of Coulomb's law. (See previous page). This states an "inverse square relationship" between a charge or illumination as the distance away from the source increases.

This means, if the distance from the source (a candle) to the object being illuminated is doubled, the light doesn't halve, it is "inversely squared. The way we illustrate this is to imagine a butter gun.

Diag 2

If the distance from the gun, which sprays a single quantity of butter at a slice of bread is one, the area covered will be one slice exactl (100 sq.cm). However if we double the distance (say the bread is 10 cm square), from 10cm (from the butter gun to the bread), to 20cm, the number of slices covered will be four, or an area 20cm by 20cm or 400cm. This is 25% or one quarter the asmount of butter on each slice, not half.

If we again increase the distance from the butter gun to the bread by 10 cm, making it 30cm, the butter spray will cover (3x3) 9 slices (900 sq. cm). Each will receive one nineth of the original slice.

As I said, this works equally with sound (volume) and light, and also electromagnetic forces, such as magnetic 'attraction'. What works on the flat, also works in a sphere.

By this you can see that as the distance from the force at the centre of an atom (a proton), which attracts, or holds the electron in place increases, the holding power diminishes.

It is important you understand this ratio of 1 to 4 is significant because it describes the shape of a Helium nucleus, which I will explain on the next page.

Don't worry too much about calculating the surface area of sphere.

A sphere can also be defined as the surface formed by rotating a circle about any diameter. If the circle is replaced by an ellipse, and rotated about the major axis, the shape becomes a prolate spheroid, rotated about the minor axis, an oblate spheroid.

Surface area of a sphere

The surface area of a sphere is given by the following formula

$\!A = 4\pi r^2.$

This formula was first derived by Archimedes, based upon the fact that the projection to the lateral surface of a circumscribing cylinder (i.e. the Lambert cylindrical equal-area projection) is area-preserving. It is also the derivative of the formula for the volume with respect to r because the total volume of a sphere of radius r can be thought of as the summation of the surface area of an infinite number of spherical shells of infinitesimal thickness concentrically stacked inside one another from radius 0 to radius r. At infinitesimal thickness the discrepancy between the inner and outer surface area of any given shell is infinitesimal and the elemental volume at radius r is simply the product of the surface area at radius r and the infinitesimal thickness.

At any given radius r, the incremental volume (δV) is given by the product of the surface area at radius r (A(r)) and the thickness of a shell (δr):

$\delta V \approx A(r) \cdot \delta r. \,$

The total volume is the summation of all shell volumes:

$V \approx \sum A(r) \cdot \delta r.$

In the limit as δr approaches zero^[1] this becomes:

$V = \int_0^r A(r) \, dr.$

Since we have already proved what the volume is, we can substitute V:

$\frac{4}{3}\pi r^3 = \int_0^r A(r) \, dr.$

Differentiating both sides of this equation with respect to r yields A as a function of r:

$\!4\pi r^2 = A(r).$

Which is generally abbreviated as:

$\!A = 4\pi r^2.$

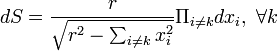Alternatively, the area element on the sphere is given in spherical coordinates by $dA = r^2 \sin\theta\, d\theta\, d\phi.$ . With Cartesian coordinates, the area element $dS=\frac{r}{\sqrt{r^{2}-\sum_{i\ne k}x_{i}^{2}}}\Pi_{i\ne k}dx_{i},\;\forall k$ . More generally, see area element.

The total area can thus be obtained by integration:

$A = \int_0^{2\pi} \int_0^\pi r^2 \sin\theta \, d\theta \, d\phi = 4\pi r^2.$

Equations in R³

In analytic geometry, a sphere with center (x₀, y₀, z₀) and radius r is the locus of all points (x, y, z) such that

$\, (x - x_0 )^2 + (y - y_0 )^2 + ( z - z_0 )^2 = r^2.$

The points on the sphere with radius r can be parametrized via

$\, x = x_0 + r \sin \theta \; \cos \varphi$

$\, y = y_0 + r \sin \theta \; \sin \varphi \qquad (0 \leq \varphi \leq 2\pi \mbox{ and } 0 \leq \theta \leq \pi ) \,$

$\, z = z_0 + r \cos \theta \,$

A sphere of any radius centered at zero is an integral surface of the following differential form:

$\, x \, dx + y \, dy + z \, dz = 0.$

This equation reflects the fact that the position and velocity vectors of a point travelling on the sphere are always orthogonal to each other.

The sphere has the smallest surface area among all surfaces enclosing a given volume and it encloses the largest volume among all closed surfaces with a given surface area. For this reason, the sphere appears in nature: for instance bubbles and small water drops are roughly spherical, because the surface tension locally minimizes surface area. The surface area in relation to the mass of a sphere is called the specific surface area. From the above stated equations it can be expressed as follows:

$SSA = \frac{A}{V\rho} = \frac{3}{r\rho}.$

mayfair

Surface area of a sphere

Equations in R3

Equations in R³