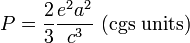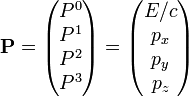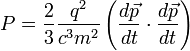mayfair

www.rainierbank.biz

Atoms

Don't worry if we have covered this and you already know it.

If it is too difficult, just study the bits you can understand, and come back to it later.

We will first start with a model of a simple atom, Hydrogen, and try to understand why atoms have the structure they do.

Bohr model of atom

In atomic physics, the Bohr model, introduced by Niels Bohr in 1913, depicts the atom as a small, positively charged nucleus surrounded by electrons that travel in circular orbits around the nucleus—similar in structure to the solar system, but with electrostatic forces providing attraction, rather than gravity. This was an improvement on the earlier cubic model (1902), the plum-pudding model (1904), the Saturnian model (1904), and the Rutherford model (1911). Since the Bohr model is a quantum-physics–based modification of the Rutherford model, many sources combine the two, referring to the Rutherford–Bohr model.

The model's key success lay in explaining the Rydberg formula for the spectral emission lines of atomic hydrogen. While the Rydberg formula had been known experimentally, it did not gain a theoretical underpinning until the Bohr model was introduced. Not only did the Bohr model explain the reason for the structure of the Rydberg formula, it also provided a justification for its empirical results in terms of fundamental physical constants.

Larmor formula

In physics, in the area of electrodynamics, the Larmor formula (not to be confused with the Larmor precession from classical NMR) is used to calculate the total power radiated by a nonrelativistic point charge as it accelerates. It was first derived by J. J. Larmor in 1897, in the context of the wave theory of light.

When accelerating or decelerating, any charged particle (such as an electron) radiates away energy in the form of electromagnetic waves. For velocities that are small relative to the speed of light, the total power radiated is given by the Larmor formula:

$P = \frac{e^2 a^2}{6 \pi \varepsilon_0 c^3} \mbox{ (SI units)}$

$P = {2 \over 3} \frac{e^2 a^2}{ c^3} \mbox{ (cgs units)}$

where $a$ is the acceleration, $e$ is the charge, and $c$ is the speed of light. A relativistic generalization is given by the Liénard-Wiechert Potentials.

Four momentum

In special relativity, four-momentum is the generalization of the classical three-dimensional momentum to four-dimensional spacetime. Momentum is a vector in three dimensions; similarly four-momentum is a four-vector in spacetime. The contravariant four-momentum of a particle with three-momentum 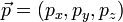$\vec p = (p_x, p_y, p_z)$ and energy $E$ is

$\mathbf{P} = \begin{pmatrix} P^0 \\ P^1 \\ P^2 \\ P^3 \end{pmatrix} = \begin{pmatrix} E/c \\ p_x \\ p_y \\ p_z \end{pmatrix}$

The four-momentum is useful in relativistic calculations because it is a Lorentz vector. This means that it is easy to keep track of how it transforms under Lorentz transformations.

(The above definition applies under the coordinate convention that $x 0 = c t$ . Some authors use the convention $x 0 = t$ which yields a modified definition with $P 0 = E / c 2$ . It is also possible to define covariant four-momentum $P μ$ where the sign of $P 0$ is reversed.)

Lam

Relativistic Generalisation

Covariant Form

We can do this by rewriting the Larmor formula in terms of momentum and then using the four vector generalisation of momentum (see four momentum), $P μ$ . We know that the power is a Lorentz invariant, so all we have to show is that our generalisation is also invariant and that it reduces to the Larmor formula in the low velocity limit. So;

$P = \frac{2}{3}\frac{q^2}{c^3m^2}\left(\frac{d\vec{p}}{dt}\cdot\frac{d\vec{p}}{dt}\right)$

Assume the generalisation;

$P = -\frac{2}{3}\frac{q^2}{m^2c^3}\frac{dP^{\mu}}{d\tau}\frac{dP_{\mu}}{d\tau}$

When we expand and rearrange the energy-momentum four vector product we get;

$\frac{dP^{\mu}}{d\tau}\frac{dP_{\mu}}{d\tau} = \frac{v^2}{c^2}\left(\frac{dP}{d\tau}\right)^2 - \left(\frac{d\vec{p}}{d\tau}\right)^2$

where I have used the fact that $\frac{dE}{d\tau} = \frac{Pc^2}{E}\frac{dP}{d\tau} = v\frac{dP}{d\tau}$ . When you let $β$ tend to zero, $γ$ tends to one, so that $d τ$ tends to dt. Thus we recover the non relativistic case.

This is an interesting equation. It says that the power radiated by the particle into space depends upon its rate of change of momentum with respect to its time. It also says that the power radiated is proportional to the charge squared and inversely proportional to the mass squared. Thus for a highly charged, extremely small particle the radiation will be much greater than that for a large particle with a small charge.

Coulomb's law or Coulomb's inverse-square law, is a law of physics describing the electrostatic interaction between electrically charged particles. It was first published in 1785 by French physicist Charles Augustin de Coulomb and was essential to the development of the theory of electromagnetism.^[1]^[2] Nevertheless, in 1767 Joseph Priestley of England conjectured that the force between charges varied as the inverse square of the distance.^[3]^[4] In 1769, Scottish physicist John Robison announced that according to his measurements, the force of repulsion between two spheres with charges of the same sign varied as x^-2.06.^[5] The dependence of the force between charged bodies upon both distance and charge had been discovered, but not published, in the early 1770s by Henry Cavendish of England, prior to Coulomb's works.^[6]

The scalar form of Coulomb's law is an expression for the magnitude and sign of the electrostatic force between two idealized point charges, small in size compared to their separation. This force (F) acting simultaneously on point charges (q₁) and (q₂), is given by

$F = k_\mathrm{e} \frac{q_1q_2}{r^2}$

where r is the separation distance and k_e is a proportionality constant. A positive force implies it is repulsive, while a negative force implies it is attractive.^[7] The proportionality constant k_e, called the Coulomb constant (sometimes called the Coulomb force constant), is related to defined properties of space and can be calculated based on the speed of light to be exactly:^[8]

Coulomb's law states that: "The magnitude of the Electrostatics force of interaction between two point charges is directly proportional to the scalar multiplication of the magnitudes of charges and inversely proportional to the square of the distances between them."

In SI units, the meter is defined such that the speed of light in vacuum (or electromagnetic waves, in general), denoted c,^[9] is exactly 299,792,458 m·s⁻¹^[10], and the magnetic constant (μ₀) is set at 4π × 10⁻⁷ H·m⁻¹.^[11] In agreement with electromagnetic theory, requiring that

${1 \over \mu _0 \varepsilon _0 }= c^2 ,$

the value for the electric constant (ε₀) is derived to be ε₀ = 1/(μ₀c²) ≈ 8.85418782×10⁻¹² F·m⁻¹.^[12] In electrostatic units and Gaussian units, the unit charge (esu or statcoulomb) is defined in such a way that the Coulomb constant is 1 and dimensionless.

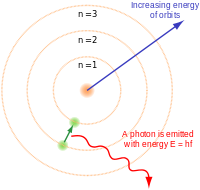
The Rutherford–Bohr model of the hydrogen atom (Z = 1) or a hydrogen-like ion (Z > 1), where the negatively charged electron confined to an atomic shell encircles a small, positively charged atomic nucleus and where an electron jump between orbits is accompanied by an emitted or absorbed amount of electromagnetic energy (hν).^[1] The orbits in which the electron may travel are shown as grey circles; their radius increases as n², where n is the principal quantum number. The 3 → 2 transition depicted here produces the first line of the Balmer series, and for hydrogen (Z = 1) it results in a photon of wavelength 656 nm (red light

This is the Lienard result, which was first obtained in 1898. The $γ 6$ means that when $γ$ is very close to one (i.e. $β < < 1$ ) the radiation emitted by the particle is likely to be negligible. However when $γ$ is greater than one (i.e. $\beta \rightarrow 1$ ) the radiation explodes as the particle tries to lose its energy in the form of EM waves. It's also interesting that when the acceleration and velocity are orthogonal the power is reduced by a factor of $\vec{\beta}\cdot\vec{\dot{\beta}}$ . The faster the motion becomes the greater this reduction gets. In fact, it seems to imply that as $β$ tends to one the power radiated tends to zero (for orthogonal motion). This would suggest that a charge moving at the speed of light, in instantaneously circular motion, emits no radiation. 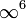However, it would be impossible to accelerate a charge to this speed because the $γ 6$ would explode to $\infty^6$ , meaning that the particle would radiate a gigantic amount of energy which would require you to put more and more energy in to keep accelerating it. This would imply that there is a cosmic speed limit, namely c. Such a connection was not made until 1905 when Einstein published his paper on Special Relativity.

We can use Lienard's result to predict what sort of radiation losses to expect in different kinds of motion.

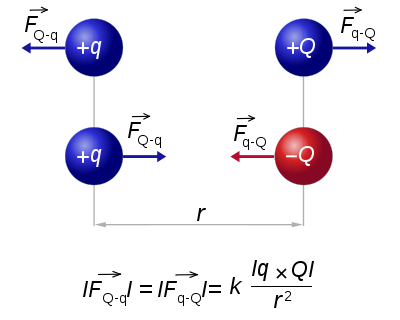
Diagram describing the basic mechanism of Coulomb's law; like charges repel each other and opposite charges attract each other.

protons 53

Relativistic Generalisation

Covariant Form