www.rainierbank.biz

   Site                 

So what happens in square (flat or two dimensional) space if we introduce the reliationship of 1 to 2 to the relationship of 1 to 4?
What I mean by this is, imagine you have two circles one inside the other. The smaller one is circumference 1, and the larger has a circumference four times as big (4).
The same will apply if they are three dimensional will it not?
If the outer one is now only twice (2 x) as big as the inner one there is suddenly not as much space between them.
If the outer space was full of something, (electrons, or charge), suddenly that has to go somewhere, or change (compress) in some way.
 If it leaves, fine, but where will it go?
If it compresses, and this may not be possible, how does its nature change?
Don't worry we will answer all these questions.

 A sphere can also be defined as the surface formed by rotating a circle about any diameter. If the circle is replaced by an ellipse, and rotated about the major axis, the shape becomes a prolate spheroid, rotated about the minor axis, an oblate spheroid.

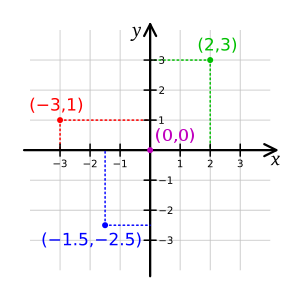
 Bi dimensional Cartesian coordinate system

Bi-dimensional space is a geometric model of the planar projection of the physical universe in which we live. The two dimensions are commonly called length and width .Both directions lies in the same plane.

In physics and mathematics, a sequence of n numbers can be understood as a location in n-dimensional space. When n = 2, the set of all such locations is called 2-dimensional Euclidean space or bi-dimensional Euclidean space.

In physics, our bi-dimensional space is viewed as a planar representation of the space in which we move, described as bi-dimensional space or two-dimensional space.

There is a theorem in mathematics which says in effect: "All shapes are ellipses". This can be proven mathematically.

It also says, "All shapes are not ellipses", and this too can be proven. Is this the theorem Dan Kalman is talking about?

 The Most Marvelous Theorem in Mathematics

by Dan Kalman


Title Page

Author Information

 An ellipse is a circle that has been stretched in one direction, to give it the shape of an oval. But not every oval is an ellipse, as shown in Figure 1, below.

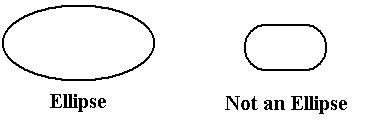
  There is a specific kind of stretching that turns a circle into an ellipse, as we shall see on the next page. Figure 2 hints at the nature of the type of stretching that creates an ellipse. Note that a typical point of the red circle is shown, as well as the corresponding point of the blue ellipse. The blue point is the result of stretching the red point horizontally by a factor of 2.

 

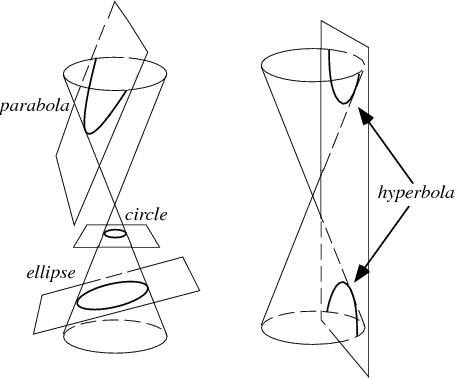
There are several alternate ways to define an ellipse. One is as the intersection of a plane with a cone. An ellipse is just one of the possible shapes for this intersection (called a conic section), as shown in the Figure 3 below, which appears at Wolfram Math World


 

 

Make a free website with Yola